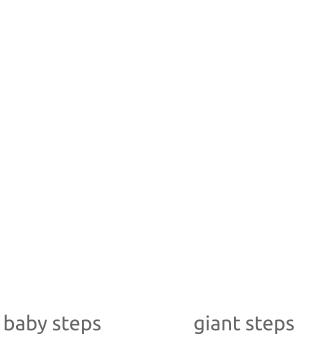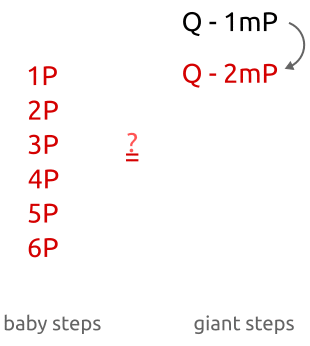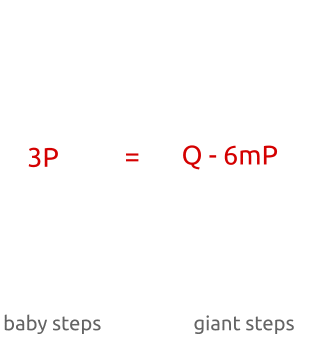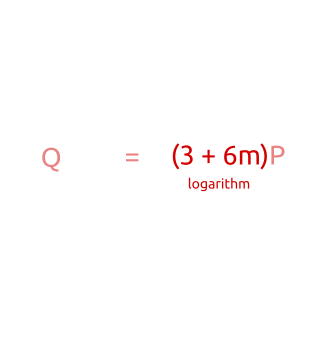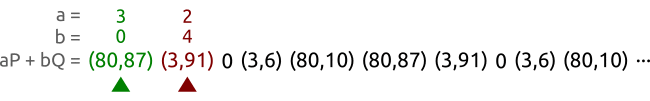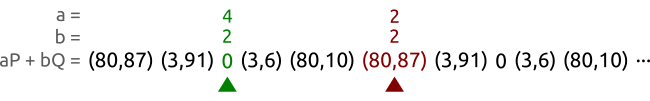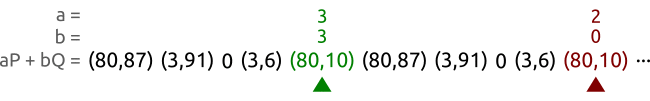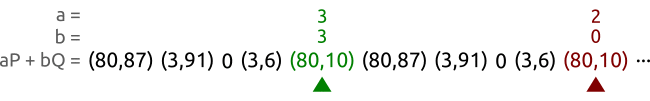ECC 椭圆曲线加密算法学习————从实数域到有限域的椭圆曲线
标签(空格分隔): ecc Crypto
****
> File Name: ECC 椭圆曲线加密算法学习————从实数域到有限域的椭圆曲线
> Author: shaobaobaoer
> Mail: shaobaobaoer@126.com
> WebSite: shaobaobaoer.cn
> Time: Sunday, 24. March 2019 11:53AM
****
0x00 前言
我好像很久没有自己学点东西了,从寒假上来就一直在做期末大作业然后考试。现在算是考完了,但是也要意味着考研复习要彻底拉开帷幕了。很多想去复现的CVE只能在计划本上越排越后面。有个东西一直想去看看,就是ECC。上学期学了数论的选修课,
参考的网站
- https://andrea.corbellini.name/2015/05/17/elliptic-curve-cryptography-a-gentle-introduction
- https://andrea.corbellini.name/2015/05/23/elliptic-curve-cryptography-finite-fields-and-discrete-logarithms/
相关代码
- 本文的完整代码
- Schoof 算法Python版本
预先准备的数学概念
群 Group
这个概念来自于离散数学,有所困惑还请多翻翻书。对于一个阿贝尔群(有些书上管它叫交换群或者加群,相信学过离散数学的你对它一定记忆犹新)它的性质包括
- 具有封闭性
- 满足结合律
- 存在单位元
- 每个数存在逆元(备注,知乎上的翻译翻错了)
- 满足交换律
整数域和有限域
首先,有限域是一个带有有限元素的集合。比如,有一个有限域是整数模p的集合(integers mod p,p是素数),可表示为 $\mathbb {Z}/p,GF(p)$ 或 $\mathbb {F}_{p}$ ,一般用后者。
模运算 mod
这个概念来自于数论,有所困惑的还请找潘兄弟俩的书看看。
需要用到的知识在下面罗列
- 模运算的加法
- 模运算的乘法
- 乘法逆元,简称逆元
- $ 45 \times x \equiv 1 (mod ;23) $
- 得出 $ x = -1 $所以,-1是45对模23的逆元
- 关于乘法逆元可以用辗转欧几里得算法来快速求出。代码在
misc/shaobaobaoer_math_lab.py下。
形如$ y^2 ;\equiv ;A;(;mod;p;)$的同余方程求解问题
参考网站
https://www.johndcook.com/blog/quadratic_congruences/?tdsourcetag=s_pctim_aiomsg
https://blog.csdn.net/ACdreamers/article/details/10182281
C代码模板:
https://blog.csdn.net/Quack_quack/article/details/50189111
其中p是一个奇素数。其中需要用到一些二次剩余得知识证明。在两篇文章中都有说,这里就记录一些结论。
确定方程是否有解?
方程有解当且仅当 $A^{\frac{p-1}{2}}\equiv 1 (mod p)$
确定方程的解
如何计算方程的解呢?
网上搜下来都是ACM的题目了。顿时感觉自己血菜。在ACMer的博客里看到了 cipolla算法。代码量用python写起来不是很复杂,但是这个东西暂时还看不懂,魔改了一下 cipolla 的模板。之后也许会填坑
三次一元方程解的形式
对于如下形式的方程
$$ ax^3 + bx^2 + cx + d = 0$$
存在如下结论
$x1+x2+x3=-b/a$
$x1x2+x2x3+x3x1=c/a$
$x1x2*x3=-d/a$
现在,方程变为如下形式
$$ (kx + c)^2 = x^3 + ax +b ;;; \Longleftrightarrow ;;;x^3 - k^2x^2 + (a-2kc)x + b - c^2 = 0$$
可以得到如下结论,该结论可以节省很多解方程的时间
$$x3= k^2 - x1 - x2$$
0x01 椭圆曲线定义
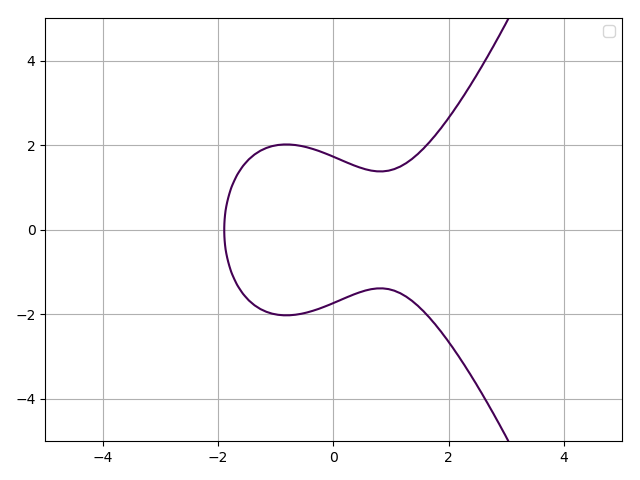
首先来看下椭圆曲线的标准形式公式:
$$y^2 = x^3 + ax +b$$
其中 $4a^3 + 27b^2 \ne 0 $ 这个限定条件保证曲线不包含奇点。
这样的椭圆曲线被称为 Weierstrass 标准形式。
当然,为了定义椭圆曲线,还需要一个无穷远的点作为曲线的一部分,在这里用符号 $\odot$ 表示。
最终,将表达式可以精炼为
$$\left{ (x, y) \in \mathbb{R}^2\ |\ y^2 = x^3 + ax + b,\ 4 a^3 + 27 b^2 \ne 0 \right}\ \cup\ \left{ \odot \right}$$
根据解析式,不难发现该曲线关于x轴对称,之后会用到其性质
1.1 标准形式的椭圆曲线绘制
执行如下代码可以画出来一个椭圆曲线。
1 | # draw_curve/draw.py |
1.2 椭圆曲线上的群G
之后,有了这个可爱的曲线之后,我们定义一个群G
- 群众元素满足上头的表达式,也就是说,群中元素是椭圆曲线上的点
- 单位元$e$是无穷远处的点$\odot$
- 逆元$p$是原坐标点关于x轴对称的那一点。
- 定义一种在该群上的加法,取一条与曲线相交于三点的直线,记交点为$P,Q,R$,他们的总和等于0,就是说$P+Q+R=0$。这三点没有顺序,所以可以证明该椭圆曲线满足交换律。
之后,可以证明这个群是一个典型的阿贝尔群。
1.3 群G上加法运算的各种情况
为了方便表示,可以把该加法写成$P+Q=-R$
这样写,其中的-R有几何含义,也就是R关于X轴对称的一点,如图

之后,讨论三种情况。
CASE 1 P = Q :
$k = \cfrac{3x^2_0 + a }{2y_0}$
得知直线方程后,计算$R_x= k^2 - x1 - x2$
CASE 2 P != Q 并且 P + Q = -R:
$k = \cfrac{y_P - y_Q}{ x_P - x_Q}$
得知直线方程后,计算$R_x= k^2 - x1 - x2$
CASE 3 P != Q 并且 P + Q = -P OR P + Q = -Q:
这就是之前说到的第三种情况,在这种情况下,只需要计算
$ \cfrac{3x^2_0 + a }{2y_0} - \cfrac{y_P - y_Q}{ x_P - x_Q} $是否等于零
这种情况下,$P,Q$必有一点满足上式。将该点坐标的纵坐标求反即得到 -R。实际运算的时候可以和CASE2合并。
之后,就可以写一个函数来计算-R的值了,在此就罗列一些关键代码
1 | def get_three_pionts(self, P, Q): |
1.4 标量积与对数问题
定义一种变量积如下所示,实际上可以用快速幂来解决这个数乘问题 $$nP = \underbrace{P + P + \cdots + P}_{n\ \text{times}}$$
OK,对于给定的$Q$($Q=nP$)和$P$是否能够找到这个n呢?当然,这玩意儿不叫除,而是叫对数。(为了和其他密码中“幂”的说法保持一致,从某种程度上而言,这个也算是幂而非数乘)
刚才说了,加法是有特殊的定义的。然而一个个加P又非常蠢,有什么好的方法呢?其中一个比较好的算法是倍加算法。原理很简单,可以看如下公式
n = 151, 二进制表示: $10010111_2$ ,这个二进制也可以表示成幂次加和:
$\begin{array}{rcl} 151 & = & 1 \cdot 2^7 + 0 \cdot 2^6 + 0 \cdot 2^5 + 1 \cdot 2^4 + 0 \cdot 2^3 + 1 \cdot 2^2 + 1 \cdot 2^1 + 1 \cdot 2^0 \ & = & 2^7 + 2^4 + 2^2 + 2^1 + 2^0 \end{array}$
简化一下:
$151 \cdot P = 2^7 P + 2^4 P + 2^2 P + 2^1 P + 2^0 P$
在之后,可以写一下小把戏来达成这个加法,bits函数其实就是一个迭代器。而每次更新P和R的值。R是最后的结果,而P则是每次自加,形如$2^n P$,n为迭代次数。
1 | def get_scalar_multiplication(self, n, P): |
在连续曲线上,这个n是非常好找的,(当然你要算很多次)但是如果在离散领域呢?就会变得更加复杂。这是椭圆曲线加密算法的核心所在。
0x02 有限域和离散对数领域的椭圆曲线
之前说了关于标量积的相关知识,在看这节之前,还需要知道数论的相关知识
之后,将椭圆曲线和有限域 $\mathbb {F}{p}$结合起来,在$\mathbb {F}{p}$上定义椭圆曲线,形式是点集。于是它变成了这样子,注意,在计算 $y^2 \equiv A (mod ;p)$的时候推荐用前文说到的cipolla算法
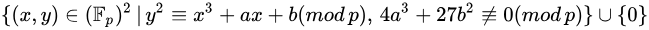
参考一些图片如下所示:这就是画出来的图
a=-7;b=10;p=19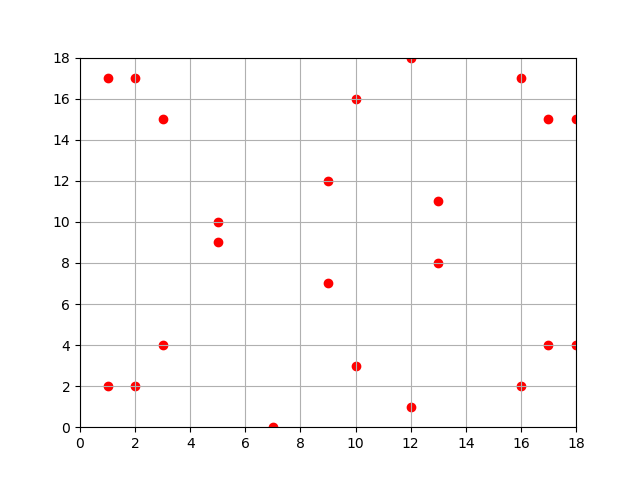
a=-7;b=10;p=97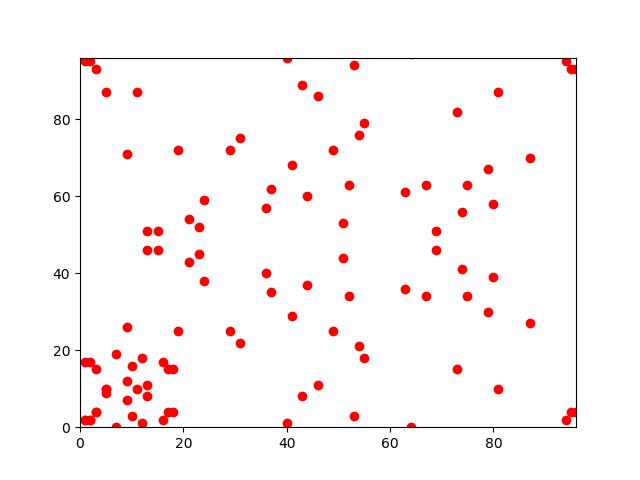
$\mathbb {F}_{p}$本身是一个阿贝尔群。不难证明对于在离散对数域内的椭圆曲线,仍然是一个阿贝尔群。【证明在最后】
另外,回到之前刚刚说的奇点,所谓奇点,就是说在曲线中会算出来在(0,0)处的点。注意我们定义的单位元$\odot $ 的位置就是(0,0)。为了不让曲线上的点与单位元重合,所以要排除掉含有奇点的曲线。比如说曲线线$$y^2 \equiv x^3 (mod;29)$$,令$x=0$,$y=\pm 0$,可以发现在(0,0)处有三个点(别忘了还有一个单位元)。所以是一个无效的椭圆曲线
2.1 离散域上点的加法
之前谈及过,$P + Q =-R$这玩意儿在实数域自然没有问题。在有限域之内也可以参照相同的定义
对此,设$L : ax + by + c \equiv 0 (mod ; p)$为$\mathbb {F}_{p}$ 上一条线。同样可以通过两点确定一条直线。
和之前证明的东西类似,只不过都需要加上$mod;p$。
对此,主要讨论之前出现的两种情况,大胆利用实数域的做法,实际上方法一样。
CASE 1 P = Q :
$k \equiv \cfrac{3x^2_0 + a }{2y_0} (mod ; p)$
得知直线方程后,计算$R_x \equiv k^2 - x1 - x2 (mod ;p )$
CASE 2 P != Q 并且 P + Q = -R:
$k \equiv \cfrac{y_P - y_Q}{ x_P - x_Q} (mod ; p)$
得知直线方程后,计算$R_x \equiv k^2 - x1 - x2 (mod ;p )$
CASE 3 P != Q 并且 P + Q = -P OR P + Q = -Q:
这就是之前说到的第三种情况,在这种情况下,只需要计算
$ \cfrac{3x^2_0 + a }{2y_0} (mod ; p) - \cfrac{y_P - y_Q}{ x_P - x_Q} (mod ; p) \equiv 0 (mod ; p)$
这种情况下,$P,Q$必有一点满足上式。将该点坐标的纵坐标求加法逆元即得到 -R。实际运算的时候可以和CASE2合并。
之后,就可以写一个函数来计算-R的值了,在此就罗列一些关键代码
1 | def get_three_pionts(self, P, Q): |
2.2 椭圆曲线阶
既然是在有限域$\mathbb {F}_{p}$内,那么椭圆曲线应该是有限个点构成的,所以,到底有多少个点呢?
对于一个群而言,有多少点就叫做这个群的阶。比如模13群的阶为 13。同样,对于有限域$\mathbb {F}_{p}$上的椭圆曲线而言,也有对应的阶。枚举当然是很蠢的,有种算法叫做Schoof算法,它的复杂度是多项式时间,算法比较复杂。可以在github上找到其代码https://github.com/pdinges/python-schoof
注意需要用 Linux 和 python3 运行,大概的用法如下所示:
1 | ➜ python-schoof git:(master) ✗ python3 naive_schoof.py 23 4 2 |
2.3 从数乘到循环子群
之前实现了连续域内的数乘,离散领域内容也是类似,利用相同的幂次加和来计算nP。唯一需要注意的就是对于n=0而言,直接返回单位元$\odot$(0,0)即可。主要代码如下:
1 | def get_scalar_multiplication(self, n, P): |
实际上还有一些优化策略,会在之后讨论。
当写完这个函数后,会发现椭圆曲线上有个很有意思特点,任取一条曲线如:
$$ y^2 \equiv x^3 + 2x + 3 (mod ;97)$$
已知点P(3,6)在该曲线上。
我们来算算 $nP$是多少。
- $0P \rightarrow \odot$
- $1P \rightarrow (3,6)$
- $2P\rightarrow (80,10)$
- $3P\rightarrow (80,87)$
- $4P\rightarrow (3,91)$
- $5P\rightarrow \odot$ 备注:计算斜率的会出现
(n * x + p * y) % p != gcd的情况,这也就意味着该点位于无穷远处 - $1P \rightarrow (3,6)$
- $2P\rightarrow (80,10)$
- $3P\rightarrow (80,87)$
- $9P\rightarrow (3,91)$
- $10P \rightarrow \odot$
不难发现P的倍乘是一个5阶循环群,生成元是$\langle \odot \rangle$,$\langle P \rangle$,$\langle 2P \rangle$,$\langle 3P \rangle$,$\langle 4P \rangle$
同时可以发现,P的加法是一个闭环。也就意味着数乘的数字是可以提取的,如下面的公式所示:
$$mP + nP = \underbrace{P + P + \cdots + P}{m\ \text{times}} + \underbrace{P + P + \cdots + P}{n\ \text{times}} = (m + n)P $$
于是,可以证明 nP的集合是椭圆曲线形成的群里的一个具有循环性质的子群(the set of the multiples of P is a cyclic subgroup of the group formed by the elliptic curve.) 这里的P是生成元,或者叫基点。
也就是说,如果我们知道它是多少阶的循环群的话,计算 nP的代码就可以更加精简。
2.4 循环子群的阶讨论
之前不难发现,P生成子群地阶是多少。之前那个P的倍乘是一个5阶循环子群,对于其他的P和曲线而言不一定适用。那么,如何去计算阶数n呢?显然用 Schoof算法不可行,毕竟它是对于一整个椭圆曲线适用,对于其子群无效。
- 设一个群G的阶为N。任取一个生成自群G的循环子群,设它的阶数是n,生成元为P, n,P 满足的条件是 nP=0 。就好像之前的 5P=0 。(这里的群说的是有限域内的椭圆曲线,只说思路,没加证明)
- P 的阶和椭圆曲线是有联系的,根据拉格朗日定理,子群的阶是父群的阶的因子。换句话说,如果一个椭圆曲线包含 N 个点,它的一个子群包含 n 个点,那么 n 是 N 的因子。
结合上述两个定律,那么n的计算可以通过如下步骤
- 用 Schoof 计算 椭圆曲线的阶 $N$
- 从小到大遍历 $N$ 的所有因子
- 找到最小的$n$ 使得 $nP = 0$
2.5 寻找子群与离散对数问题
之前讨论了很多椭圆曲线上的东西。那么,如何利用ECC去加密解密呢?
首先补充一点拉格朗日定理的东西。拉格朗日定理证明$h = N/n$永远是一个整数,称 $h$为辅因子。引入$h$。那么可以得到$n(hP)=0$
由此,总结一下ECC的算法步骤
- 计算椭圆曲线的阶 $N$
- 选择一个阶为 $n$ 的子群,n为素数且为$N$的因子。
- 计算辅因子 $h = N/n$
- 在曲线上选择一个基点 P
- 计算 $G = hP$
- 如果G是0,那么重新选择基点否则找到了阶为$n$,生成元为$P$的子群
现在,假设有一条的在有限域$\mathbb {F}_{p}$上的椭圆曲线,要解决的问题是:
如果我们已知 P和Q ,对于 Q = kP ,我们应该怎么去计算这个 k ?
这个是椭圆曲线中大名鼎鼎的离散对数问题。也是其最为核心之处。
ECC有趣的地方在于,它的离散问题看上去比其他密码学中的离散问题难多了。这就说明我们可以用更少的位数的整数 k 做到和其他加密算法一样安全级别的加密效果。