ECC 椭圆曲线加密算法学习————ECDH与ECDSA

Posted on

ECC 椭圆曲线加密算法学习————ECDH与ECDSA

标签（空格分隔）： ecc Crypto

****
> File Name: ECC 椭圆曲线加密算法学习————ECDH与ECDSA
> Author: shaobaobaoer
> Mail: shaobaobaoer@126.com
> WebSite: shaobaobaoer.cn
> Time: Sunday, 25. March 2019 22:42PM
****

<!–查看注释有惊喜–>

0x00 前言

之前学习了实数域上的椭圆曲线与有限域$\mathbb {F}_{p}$上的椭圆曲线。详细可以参考ECC椭圆加密算法学习————从实数域到有限域的椭圆曲线。

不难发现，在实数域的标量乘法看上去是一个“简单”的问题，但是在有限域$\mathbb {F}_{p}$就显得非常困难。本文主要讨论如何将之前所学的运用于加密问题中。

相关代码

一些重要的域参数

  • 素数 $p$
  • 椭圆曲线系数 $a$ 与 $b$
  • 基点（生成元） $G$
  • 子群的阶$n$
  • 辅因子$h$

之后，将这六个域参数组合成一个一个六元组$(p,a,b,G,n,h)$

在后文中会经常用到

本文代码

0x01 椭圆曲线加密算法

尽管之前花了很长时间的铺垫，但是椭圆曲线的密码学策略，简单而纯粹

在选取完毕一个六元组后，定义如下内容

  • 私钥： 一个随机的整数$d$，选取自${1,…,n-1}$
  • 公钥：$H = dG$ （$G$是循环子群的生成元）

至此，来考虑一个问题
如果我们知道 $d$与六元组，那么很简单就可以算出$H$了。但是，如果我们只知道$H$和$G$，去寻找一个$d$是非常困难的，因为这需要解决离散对数问题。

通过这一组密钥，可以衍生出两种经典的椭圆曲线加密算法，分别是 ECDH，可以用来加密。以及 ECDSA ，可以用来数字签名

0x02 ECDH 加密算法

ECDH是Diffie—Hellman算法的衍生。关于DH算法这里不展开，如果能学到这里想必对DSA与DH都有一定程度的了解。

2.1 ECDH 的工作过程

ECDH的工作原理如下所示，实际上和纯粹的DH算法有着非常相似的地方

  • Alice 和 Bob 首先约定一个六元组，生成自己的私钥和公钥。定义数据结构如下
    • Alice Private Key : $d_A$
    • Alice Public Key : $H_A = d_AG$
    • Bob Private Key : $d_B$
    • Bob Public Key : $H_B = d_BG$
  • Alice 和 Bob 公开得交换公钥。第三方可以窃听到 公钥$H_A$和$H_B$，但是他无法解出$d_A$和$d_B$
  • Alice 用自己的私钥计算 $S_A = d_A H_B$；Bob 用自己的私钥计算 $S_B = d_B H_A$

很显然 $S_A = S_B$ 因为以下算式

$$S = d_AH_B = d_A(d_B G) = d_B(d_A G)$$

对此，可以将上述过程总结为一个数学问题。

给定三个点 P,aP,bP,那么abP的结果是什么？

总之，ECDH的问题也被归结为非常困难的那一类。尽管无法证明有多困难，但是这个难度应该和在上一篇文章最后提及的椭圆曲线难题的难度相当。

  • 此时，Alice和Bob已经获得了共享密钥，可以通过对称加密来交换数据

比如说，他们可以使用S的x坐标密钥，使用AES或者3DES加密消息。
实际上在TLS的过程中中，TLS将x坐标与其他相关的数字关联起来，从而计算得到字节型字符串的散列。

2.2 ECDH 加密解密实践

之前为了解释算法的过程，所以采用了非常简单的椭圆曲线。实际上，运用在实际中的曲线非常复杂。有一个组织叫高效密码学标准协会SECG。制定了一系列的高强度的密码学标准。可以在相关文档中查到高强度的密码学参数。

在此，选取了Secp256k1作为之后演示的例子。同时secp256k1也是比特币公钥加密中的椭圆曲线参数。
其六元组的构成如下所示:

1
2
3
4
5
6
7
p  = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
a = 0
b = 7
xG = 0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
yG = 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
h = 1

通过一个简单的脚本，可以还原上述过程，如果一切顺利，S_A 与 S_B 无论如何都是相等的

1
2
3
4
5
6
7
Curve: secp256k1
Alice's private key: 103578888203905683147310628925141324706004210586941582062255108435073330635559
Alice's public key: (72205313168121137722470139642970359323314163425341806818266474706052417395420, 42908651374588414209406038144703625728727324613824233811609705542553632995837)
Bob's private key: 97727733532815547475289836254065376178409286030674739848985976984975775000167
Bob's public key: (5226211608039988834249916327528388136314009566006478722042576040985411258297, 76867928087387169315809382707245048142671884194759753857442364958995784506075)
Shared secret calculate by Alice : (90402392865121638378190357760493775057772079441731676814490847255017097141119, 29964306249717728516272468678674342055122755840848542530168745390980111134510)
Shared secret calculate by Bob : (90402392865121638378190357760493775057772079441731676814490847255017097141119, 29964306249717728516272468678674342055122755840848542530168745390980111134510)

2.3 临时(Ephermeral) ECDH

ECDHE 也是一种常见的ECDH算法。其中的E表示短暂的。指交换的密钥是临时的，而不是静态的。在TLS中使用ECDHE。那么客户端和服务端在建立连接时即时生成其公钥私钥对，然后使用TLS证书对密钥进行签名，然后在各方之间交换

0x03 ECDSA 加密算法

ECDSA 的使用场景如下：
Alice想要用她的私钥$d_A$对一个消息进行签名。Bob希望通过Alice的公钥$H_A$来验证对消息的签名。但是只有Alice能够签名，其他人只能验证她的签名。

同样Alice和Bob使用相同的六元组域参数。所谓ECDSA是应用于椭圆曲线的DSA数字签名算法的变体。
关于DSA的具体细节，可以看看我之前写的文章（PS: 代码有些问题，当初连模逆运算都不是很懂）

ECDSA处理的是消息的哈希值，而不是消息本身，散列函数选择取决于双方，但是应当选用安全的散列函数。在此，我们定义消息的散列值为$z$

3.1 ECDSA 的签名过程

ECDSA 的流程如下所示：

预定完毕一个六元组后，Alice首先定义公钥和私钥

  • 私钥： 一个随机的整数$d_A$，选取自${1,…,n-1}$
  • 公钥: $H_A = d_AG$ （$G$是循环子群的生成元）

随后，Alice 定义如下内容

  • 选取一个随机的整数$k$，选取自${1,…,n-1}$
  • 计算 $P = kG$ （$G$是循环子群的生成元）
  • 计算 $r \equiv x_p ;(mod ;n );$ ($x_p$ 是P的横坐标)
  • 如果 $r = 0 $ 则重新选取k
  • 计算 $s \equiv k^{-1} ( z + rd_A); (mod;n)$ ($d_A$是Alice的私钥，$k^{-1}$是$k$的逆元)
  • 如果 $s = 0 $ 则重新选取k
  • 将 $(r,s)$ 封装为一个签名

简单来说，该算法生成了一个密钥k。该密钥通过标量积隐藏在签名的$r$中。之前也说过，通过$P$和$G$计算$k$，是有限域椭圆曲线的数学难题。
随后$r$通过算式 $s \equiv k^{-1} ( z + rd_A); (mod;n)$与消息散列$z$建立起联系。并将$r$和$s$封装为签名。

为了计算$s$，需要知道$k$的对于$n$的逆元。在之前说到过，如果$n$是个合数，那么在计算模逆的时候会出些一些非常棘手的状况。所以如果私钥不是素数，那么ECDSA就不能够被使用。当然，在制定高强度密码学标准的时候，自然是考虑到了这种情况

3.2 ESDSA 的验证过程

对于Bob而言，他知道$z$和$(r,s)$，可以这样来验证签名

  • 计算 $u_1 \equiv s^{-1} z ;(mod ;n)$
  • 计算 $u_2 \equiv s^{-1} r ;(mod ;n)$
  • 计算 $P_0 = u_1G + u_2H_A$
  • 当且仅当 $ r=xP;mod;n $的时候 $P_0 = H_A$

3.3 ESDSA 的正确性验证

首先从最后一步开始：（严谨而言下面每个式子都需要模n）
$$
\begin{eqnarray}
P =& u_1G + u_2H_A \
=& u_1G + u_2d_AG\
=& (;u_1 + u_2d_A; ); G
\end{eqnarray}
$$

之后回带 $u_1$,$u_2$
$$
\begin{eqnarray}
P =& (;u_1 + u_2d_A; ); G \
=& (;s^{-1} z + s^{-1} rd_A;) ;G\
=& s^{-1}(;z + rd_A;); G
\end{eqnarray}
$$

∵ $s = k^{-1}(;z + rd_A;); mod ; n $
∴ $ k = s^{-1}(;z + rd_A;); mod ; n$
因此的得证 $ P = kG$

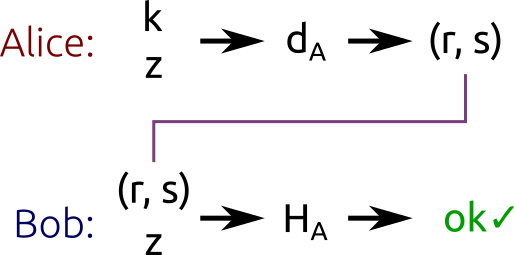
综上所述，可以将ECDSA的过程用下图来概括

image_1d6nq8u9u1vd1lro1aqn10bh1ugug.png-19.8kB

3.4 ESDSA 签名与验证演示

我写了一个ESDSA签名与验证的脚本，其输出内容如下所示。详细代码可以再github里查看

1
2
3
4
5
6
7
Curve: secp256k1
Private key: 104402155858234843462820049838931863424340700345639408070129091750274190501639
Public key: (26871662523956236501334015334554552355718345422423650192015494443518483271191, 78585437455917839772708635641693122787004414694759872862060571807949572029114)

Message: 79600447942433
Signature: (90544279873496095960562757005038315753760612769739282803554290388042828042546, mpz(81447758399901905504654585382621756821500911503165874513424939904998314198491))
Verification: signature matches

3.5 ESDSA 简单攻击演示

生成ECDSA签名时，保守秘密非常重要 ķ真的很秘密。如果我们使用相同的ķ来签名，或者如果随机数生成器可预测，攻击者就能找到私钥

如果使用相同的k进行签名，将会发生一些有趣的事情。也是索尼在11年前犯的错误

在计算开始之前，首先我们应当知道域参数的六元组（或者曲线名称），两组签名 $(r_1,s_1),(r_2,s_2)$与哈希值$z1$,$z2$。以及公钥 $S_A$

对于相同的k生成的两组签名 $(r_1,s_1),(r_2,s_2)$而言。

  • 最先确定的是$r1=r2$
  • 两式相减可得 $$s_1 - s_2 \equiv k^{-1} \times (z_1 -z_2) ; mod ;n$$
  • 两边同乘k后将k的系数除过去 可得 $$k \equiv (s_1 - s_2)^{-1} \times (z_1 -z_2) ; mod ;n$$
  • 此时，就可以计算出$k$，再利用 $k$ 可以计算出私钥$d_A$
    $$s \equiv k^{-1} (z _ rd_A) ; mod ; n \Longrightarrow d_A \equiv r{-1} (sk -z ) ; mod ; n$$